企业管理论文模板代写：危险品运输风险度量、网络优化与安全监管博弈探讨

本文是一篇企业管理论文，本文研究了蓄意攻击背景下危险品运输安全监管演化博弈问题。首先构建了政府-企业-攻击者三方的演化博弈，对均衡策略进行初步分析；其次引入了政府动态惩罚机制和动态惩罚-补贴机制，采用系统动力学仿真分析了动态惩罚机制和动态惩罚-补贴机制下的局中人的演化稳定策略。

第一章绪论

1.1研究背景及意义

1.1.1研究背景

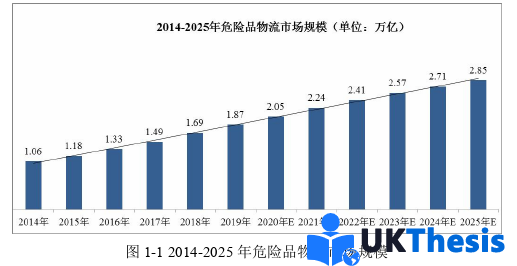
聚焦我国经济发展，工业发展是促进经济增长重要因素。根据《2019年国民经济和社会发展统计公报》，我国全年全部工业增加值为317,109亿元，相比2018年增长了5.7%。其中，化学原料和化学制品制造业比上一年增长了4.7%[1]。众所周知，化学原料和化学制品包括广泛的危险化学品（以下简称危险品），例如石油、天然气、一氧化碳等，所以化工行业的发展直接带动了危险品运输业的发展。《2020年中国危化品物流行业年度运营报告》（以下简称报告）显示，基于2014-2019年危险品物流市场规模的预测，2020-2025年我国危险品物流市场仍然呈增长趋势[2]，见图1-1。报告显示，2020年，危险品物流市场规模或超过2万亿元。在运输能力方面，道路运输量可达12亿吨，铁路运输量达1.3亿吨以及水路运输量达4亿吨，显然道路运输是这3种危险品运输方式中最主要的运输方式，占比约为69%，见图1-2。

1.2文献综述

1.2.1危险品运输问题研究

危险品运输问题属于运筹优化领域的一个子应用研究问题。危险品运输问题因危险品的有害性质，例如有毒、易燃、易爆、易腐蚀等，一直受到广大研究人员和社会人士的热切关注。早期，Peirce和Davidson在1982年率先提出了危险废物运输的线性规划研究[11]，List等详细讨论了1980年以来危险材料运输中风险分析、路由与调度和设施位置等领域所做的研究及方法，总结了单一目标优化到多目标的研究，指出了将风险分析与路由相结合的工作案例和路由与设施位置相结合的工作案例[12]。1987年，加拿大学者Fredericton组织了关于危险气体运输和储存中主要风险的国际会议，拉开了危险品运输的研究帷幕，会议的多个讨论主题围绕风险评估展开[13]。2007年，Erkut等从研究内容角度将危险品运输问题分解为风险评估、路径规划、设施与路径规划和网络设计的研究问题[14]。为了掌握近年来危险品运输问题的研究概况，本文首先对相关研究进行文献计量分析。以美国科学情报研究所(Institute for ScientificInformation，简称ISI)开发的Web of Science网站作为文献检索系统，选择SCI、SSCI、A＆HCI、CPCI为引文数据库，使用“危险品”和“运输”的英文及其扩展英文的组合作为关键词进行搜索，检索关键词及结果见表1-1。其中，符号*表示对应单词的扩展词语。例如，“rout*”可以检索出“routs”、“routing”等以“rout”为词根的词语。检索文献通过去重筛选共得到326条数据。下面采用Citespace软件对所得数据库进行文献计量分析。

第二章理论基础

2.1图与网络

在图与网络中，图是可以反映对象之间关系的一种工具[89]。其中，“对象”可以是城市、工厂、人、道路路口等，“关系”可以是贸易关系、逻辑关系、业务关系、连通关系等。图由节点和连接节点的线段构成。一般地，“对象”由节点表示，“关系”由线段表示。图可以根据边的方向性分为有向图和无向图。拓扑（Topology）是一种不考虑物体的大小、形状等物理属性，而仅仅使用点或者线描述多个物体实际位置和关系的抽象表示方法。拓扑理论因为不受物理因素的影响，关注多个物体之间的相互关系而应用广泛。从以上定义可以看出，图与拓扑本质上有一定的相似性。1736年，瑞士的数学家Leonhard Euler在论文中基于拓扑理论解决了著名的七桥问题，开启了网络拓扑（Network Topology）的新纪元[89]。1845年和1847年，Gustav RobertKirchhoff先后将网络拓扑拓展到电网络，进一步丰富了网络拓扑的应用领域。

目前，网络拓扑结构已经被学者广泛用于研究中，例如，能源领域，蔡巍等基于能源互联网的基础信息构建了网络拓扑，研究了从国家到区域级网络拓扑结构模型[90]；金融领域，何奕等针对复杂金融网络中的问题，构建了4种网络拓扑结构，研究发现不同的网络拓扑结构对系统性风险影响较为明显[91]；社交网络领域，贺瑞芳等在社交媒体的特定话题研究中，突破了仅基于纯文本的摘要研究法，提出了社交网络结构特征与文本内容相结合的摘要研究法，该方法发现社交网络的拓扑结构显著影响了话题的传播途径[92]；公交网络领域，裴玉龙等在研究城市公交网络均衡性问题时，提取网络中节点的度及其强度作为公交网络的重要表征，结合道路布局构建了二分网络[93]；道路网络领域，宋小冬等评价公共交通时，借鉴网络拓扑理论中中间度指标的计算方法，计算道路网络中影响交通适宜性的指标[94]。在危险品运输领域，Zhong等在研究运输网络的风险脆弱性评估模型时，分析了道路网络拓扑结构，使评估模型考虑风险因素的同时兼顾网络拓扑结构的影响[18]。由此可见，在不同的可以依托网络关系进行研究的科学问题中，网络拓扑分析存在着广阔的探索空间，助力提升研究问题的空间层次和逻辑结构。

2.2双层规划

双层规划本质上是双层决策问题的数学模型，由Bracken和Mcgill在1973年的研究中首次提出[96]，由Candler和Norton在1977年在研究中正式提出[97]。一般地，上层决策是双层规划问题的指导者、领导者或先行者；下层决策是双层规划问题的被指导者或跟随者。上层规划是全局角度的决策，下层规划的决策依赖于上层规划的决策，两层均有各自独立的目标函数及对应的约束条件。

双层规划的求解算法相对较多，其中关于线性规划的求解算法有极值点搜索法、分支定界法、互补旋转法等；非线性规划的求解算法有下降算法、罚函数法、智能优化算法（如模拟退火算法、遗传算法等）、神经网络算法、信赖域算法、极大熵法和混沌优化法等[101]。

双层规划模型已经广泛应用于设施选址、交通网络设计、公交调度等问题中。例如，项寅研究了上层政府选址和下层恐怖分子攻击的反恐应急设施选址问题[77]；黄露研究了配送中心选址问题，上层是企业的配送中心选址规划，下层是顾客对配送中心的选择规划[98]。李玉祺等将双层规划应用到交通网络设计领域，其中上层决策者为网络规划者，下层决策者为网络使用者[99]。慈玉生等在公交调度领域应用双层规划理论，研究了上层规划为乘客候车函数和下层规划为公交车数量函数的调度问题[100]。在危险品运输领域，王伟等在道路规划中上层考虑政府对车辆的限速规划，下层研究车辆的运输路径规划[38]；张圣忠和余永骎研究了专用车道的双层规划问题，在每层规划中分别构建了多个目标函数，其中上层规划考虑了成本、风险和车道利用率，下层规划考虑了危险品车辆与普通车辆的流量分配[46]。李奇等采用收费策略设计运输网络，上层规划的目标是最小化总风险，下层规划的目标是最小化车辆运输成本[47]。通过以上文献看出，双层规划模型研究在多主体决策和多目标规划的问题中发挥着重要作用。

第三章基于改进引力模型的危险品运输风险度量研究...........................25

3.1引言...........................................25

3.2引力模型........................................25

第四章改进风险度量下危险品运输网络优化研究...................................37

4.1引言.....................................37

4.2问题描述.................................37

第五章动态改进风险度量下危险品运输网络优化研究...........................55

5.1引言..............................................55

5.2问题描述........................................55

第七章蓄意攻击背景下危险品运输安全监管演化博弈研究

7.1引言

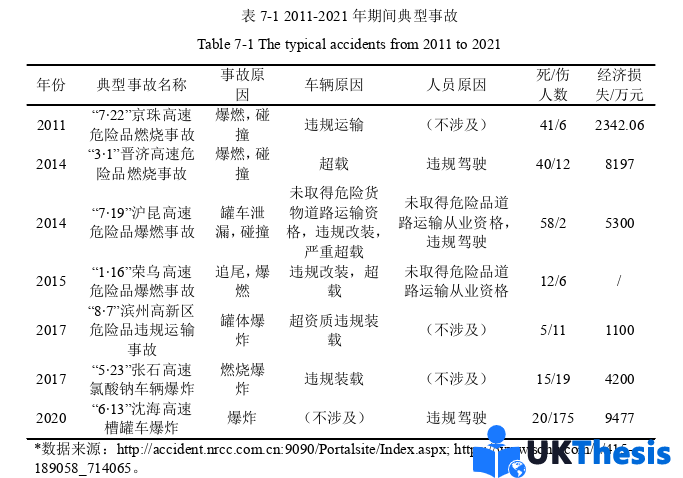
危险品运输量的快速增长一方面标志着化工行业的迅猛发展，为社会经济发展保驾护航；另一方面，危险品运输事故对人民生命财产安全也可能造成严重的后果。为了保障人民生命、生活安全，我国政府于2014年、2020年相继颁布了《加强危险品运输安全监督管理的若干意见》和《全国危险化学品道路运输安全集中整治方案》（以下简称《方案》）等法律法规，旨在加强危险品运输的严格监管。然而，根据表7-1中2011-2021年间几起典型危险品运输事故可以发现，危险品运输监管过程仍存在漏洞，部分危险品运输企业仍存在安全意识薄弱的现象。更为严重的是，蓄意攻击自20世纪90年代以来成为一个世界瞩目的现象。诸如2001年美国“9·11”事件等恐怖攻击造成的历史悲剧已给各国政府敲响警钟，提醒安全监管部门，蓄意攻击是一个不可忽视的重要因素。由于政府部门加强了对设施的防护，攻击者将攻击对象转向地面交通[5]。鉴于危险品事故具有危害性强等特点，在途危险品可能成为攻击者的新目标[6,8]。基于此，本文重点考虑了潜在蓄意攻击情况下政府对危险品运输企业的安全监管问题，旨在为安全监管部门监管方案设计提供了一定的参考。

第八章结论与展望

8.1研究结论

危险品运输量的快速增长一方面标志着化工行业的迅猛发展，为社会经济发展保驾护航；另一方面也增加危险品运输事故发生的机率，给事故附近的人和环境等因素造成损害。此外，蓄意攻击是不可忽视的危险因素，一旦攻击者瞄准防御能力薄弱的危险品运输，将会对社会公众造成影响和损失。考虑以上背景，本文研究了危险品运输的空间风险度量问题，基于双层规划的危险品运输网络优化问题，动态改进风险下危险品运输网络的双层优化问题，考虑蓄意攻击背景下政府安全防御博弈问题和安全监管问题。主要研究结论如下：

（1）研究了改进引力模型的空间风险度量模型。基于传统引力模型，引入了危险品运输风险评估中的4个关键风险因素，并融合了安全因素和道路网络的拓扑特征，构建了改进引力模型的空间风险评估模型。以北京市某局部区域的路网数据为例，分别构建了以最短距离、最小人口风险和最小改进风险为目标的路径规划问题，采用Dijkstra算法进行求解，其结果表明以本文改进的引力模型的危险品运输风险评估模型的改进风险和社会风险均最小。

（2）研究了政府阻断策略下危险品运输网络优化问题。为保障危险品道路运输安全，构建了改进风险下危险品运输路网安全的双层规划模型。其中上层规划的目标为政府决策道路服务水平下的阻断策略；下层规划是企业依据政府的阻断策略，结合危险品运输任务和成本，决策车辆服务的需求点和车辆运输路径。以不同的阻断策略进行情境划分，经过研究发现，当政府的阻断策略为柔性策略时，特定道路服务水平下政府存在多种阻断策略且企业的最优服务路线保持不变。该结论表明，在保证道路服务水平下，政府和企业仍然可以协商使双方得益同时达到最大化。

（3）研究了动态改进风险下危险品运输网络优化问题。在运输网络中，存在着人口集中的路段，而这些路段附近的人口数量随时间变化具有明显的潮汐特征，因此风险也随之变化。基于潮汐特征提出了动态零和风险的定义，构建了动态零和风险的双层规划问题。上层规划中，政府根据不同离散时间段内风险变化和最低道路服务水平，采用精确算法，确定各个时间段道路的最大阻断策略集合；下层规划中，企业根据各个时间段内政府的阻断策略和动态风险变化，采用改进的遗传算法，规划最优运输路线及路径。对于给定的道路网络和参数，采用调研数据进行数值算例研究。在时间段[0:00,7:00]和[20:00,24:00]，政府决策道路的服务水平为73.08%时，找到全局最优决策。

参考文献（略）